数据结构之树状数组
定义
如果我们要求一个数组内任意区间的和,最朴素的算法是每次对区间所有元素进行求和运算,时间复杂度为。也可以考虑用前缀和的方式去实现,求和运算的时间复杂度为,但这样一来,如果对数组的某一项进行修改,则要同步维护前缀和数组,这会导致更新操作的时间复杂度由原来的提升为。如果数据量非常巨大,这样的时间复杂度仍然是不被接受的。
树状数组则采用了一种折中方案,它通过将数组进行分组,使得求和与更新的时间复杂度均为。
引用自百度百科:
树状数组或二叉索引树(英语:Binary Indexed Tree),又以其发明者命名为Fenwick树,最早由Peter M. Fenwick于1994年以A New Data Structure for Cumulative Frequency Tables为题发表在SOFTWARE PRACTICE AND EXPERIENCE。其初衷是解决数据压缩里的累积频率(Cumulative Frequency)的计算问题,现多用于高效计算数列的前缀和, 区间和。
构造
我们以一个长度为16的数组为例,比如[6,7,4,3,6,2,8,9,3,1,9,0,5,2,1,7],我们用这个数组来构建一个树状数组,注意:为方便计算,树状数组的索引从1开始。
树状数组也是一个数组结构,并且它的长度和原始数组的长度相同。我们假设有一个树状数组为BinTree,它的每一项的值BinTree[i]表示为以索引i作为结尾并且长度为lowbit(i)的子序列之和(本例为求和,所以存储的是子序列之和)。
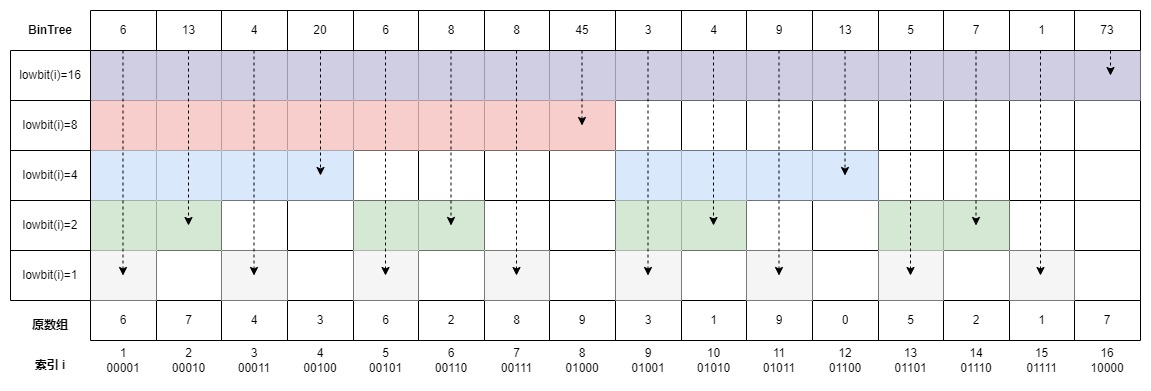
其中,lowbit函数的输入为一个任意整数,输出为这个整数最低位的1所代表的数值。例如,lowbit(12),12的二进制表示为1100,最低位的1为100,也即十进制的4,所以函数输出为4。这里传递的入参为数组索引。
lowbit函数就是树状数组的灵魂所在,稍后我们就能看到树状数组如何巧妙的利用该函数,将查询和更新操作的时间复杂度降低为的。
核心函数
lowbit
利用二进制的补码性质,我们用一行代码即可实现lowbit函数的目标。
1 | |
假设num为12,它的二进制我们用8位表示为0000 1100,则-num的二进制补码表示为1111 0100,二者相与得到0000 0100,除了最低位的1仍然保留,其余位全部变为0,这正是我们要的结果。

查询
树状数组可以以的时间复杂度求出任意长度的前缀和。比如求区间[1,11]之和,我们可以把区间分成[1,8],[9,10]和[11,11]然后再相加,而这3个区间的和已经存储在树状数组中。参考下图:
![区间[1,11]之和](/postimgs/binaryindexedtree/2.jpg)
通过观察可以发现,11的二进制表示为1011,其中包含3个1位,所以被划分为3个区间,3个区间的末尾索引分别为11(0b1011),10(0b1010)和8(0b1000),同时它们的长度分别为lowbit(11)=1,lowbit(10)=2和lowbit(8)=8,这3个区间正好覆盖了前11个元素。
所以,当前区间只要减去一个lowbit,即可得到上一个区间:11(0b1011) -> 10(0b1010) -> 8(0b1000)
我们用ask函数来表示查询方法,代码表示为:
1 | |
用自然语言可描述为,求以索引i结尾,并且长度为lowbit(i)的区间之和,接着去除索引最低位的那个1,相当于排除掉了lowbit(i)个数值,同时得到一个缩小的新索引。该问题变成了一个相同但规模更小的子问题,可用递归实现。
![区间[1,14]之和](/postimgs/binaryindexedtree/3.jpg)
利用该方法,我们可以用对数时间求得任意前缀和。现在,对于任意区间的和,我们只需计算出2个前缀和,然后相减即可得到结果。比如求区间[4,9]之和,我们分别计算出[1,9]和[1,3],再将2者相减。
更新
对于更新来说,如果我们更改了数组中的某个元素值,则所有树状数组中覆盖了该元素索引的区间都应该被更新。同样,我们可以利用lowbit规律,快速进行更新。值得注意的是,由于树状数组并没有存原始数组的值,所以我们只能更新差异值,而不是直接覆盖。
举个例子,如果我们现在把原数组中索引9的值由3改成5,则差异值为+2,则树状数组中覆盖了索引9的区间都应该+2,这些区间在树状数组中对应的索引分别为9,10,12,16。
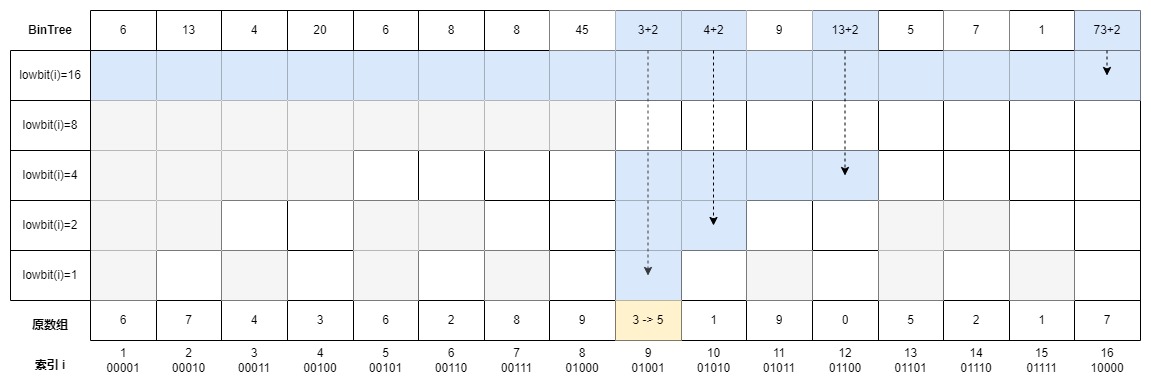
观察可发现,当前区间加上一个lowbit,即可得到上一个区间:9(0b1001) -> 10(0b1010) -> 12(0b1100) -> 16(0b10000)。
同理,更新原数组索引7,覆盖了索引7的区间的末尾索引分别为7,8,16:
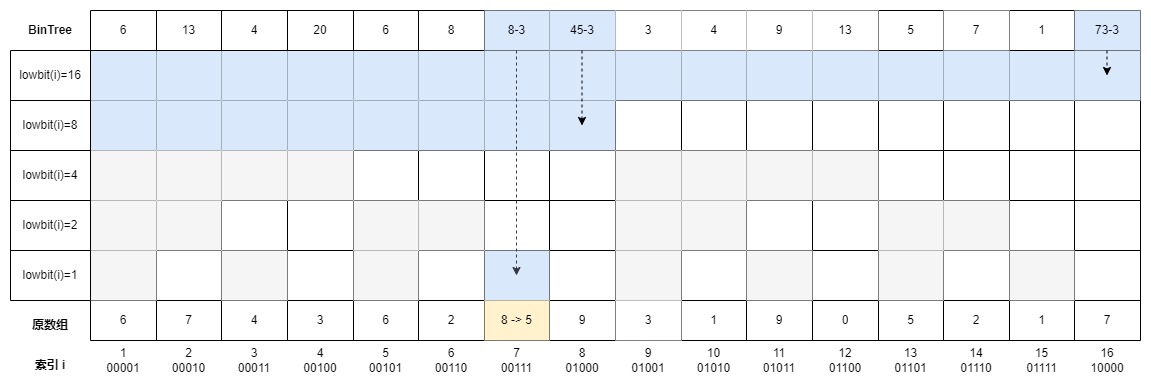
区间更新路线为:7(0b0111) -> 8(0b1000) -> 16(0b10000)。
我们用add函数来表示更新方法,代码表示为:
1 | |
自然语言描述为不断向上寻找更大的覆盖区间,直到超出最大索引。
初始化
因为树状数组的索引从1开始,所以我们构建的树状数组长度相比原数组多1个,树状数组的索引相较于原数组索引需加上1。树状数组的初始值均为0,通过add方法将原数组的每个值添加进树状数组从而进行初始化。
1 | |
扩展
我们再为这个树状数组扩展2个通用方法,更新数组和任意区间查询,以解决我们开头抛出的问题。
1 | |
现在我们就可以用树状数组来封装一个普通数组,可以对数组索引进行更新,也能查询任意区间[left,right]之和。
1 | |




